Nghịch lý Zeno (Asin ngáo đá)
“Trong một cuộc chạy đua, người chạy nhanh nhất không bao giờ có thể bắt kịp được kẻ chậm nhất. Kể từ khi xuất phát, người đuổi theo trước hết phải đến được điểm mà kẻ bị đuổi bắt đầu chạy. Do đó, kẻ chạy chậm hơn luôn dẫn đầu.”
Ví dụ cụ thể:
“Achilles chạy đua với một con rùa. Anh ấy chấp con rùa 100 mét. Anh có vận tốc nhanh gấp 10 lần con rùa. (Vận tốc của cả Achilles và rùa đều không đổi).
Ta có thể thấy:
Sau một khoảng thời gian hữu hạn, khi Achilles đã chạy được 100 mét (tức đến điểm xuất phát của con rùa) thì con rùa cũng đã chạy được thêm 10 mét. Sau một khoảng thời gian nữa, khi Achilles đã chạy được 10 mét, con rùa cũng đã nhích thêm được 1 mét.
Nói cách khác, bất cứ khi nào Achilles đến vị trí cũ của con rùa, thì con rùa lại đi thêm được một đoạn. Bởi vì số lượng các điểm đó là vô hạn, anh ta không bao giờ bắt kịp được con rùa.”
Giải đáp:
Một số người đã chứng mình nghịch lí này sai bằng cách … tổ chức một cuộc thi với rùa, và hiển nhiên là chỉ sau một khoảng thời gian ngắn, họ đã vượt qua đối thủ.
Tuy nhiên, điều này không chỉ ra được lập luận của Zeno sai ở đâu. Nói cách khác, ta biết rằng nó sai (What) nhưng không biết tại sao nó sai (Why).
Vậy lập luận của Zeno đã sai ở chỗ nào?
Để tìm ra lỗi sai, đầu tiên ta cần “công thức hóa” suy luận.

Có thể thấy rằng Zeno đã lừa chúng ta khi thay đổi bản chất bài toán. Thay vì tìm thời điểm mà Asin “vượt qua” Rùa, ông ta chỉ tìm những thời điểm mà Asin “chạy vào vị trí cũ của Rùa” (t1, t2, t3, t4, vv). Chính vì điều này, bài toán sẽ trờ thành vòng lặp vô tận (Asin đến chỗ Rùa thì Rùa đã đi).
Nói cách khác, mỗi lần Asin đến “vị trí cũ” của Rùa, anh ta sẽ đứng lại (thay vì chạy tiếp) và bài toán sẽ được “reset” lại từ đầu.
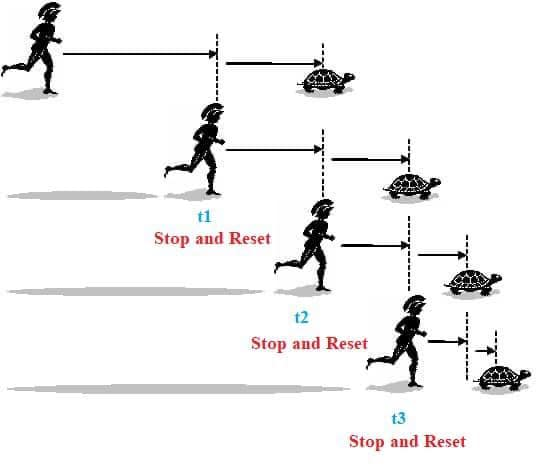
Chính vì lí do này, thay vì “nghịch lí Zeno”, mình sẽ gọi bài toán là “Asin ng’áo đá”.
Bài học rút ra:
Khi đã tìm thấy “mục tiêu” trong cuộc sống, đừng dừng lại nếu không muốn bị chửi là ng’áo đá Một học sinh lớp 10 cũng có thể giải được mấy câu đố triết học.